天下一プログラミングコンテスト2013 予選B

D. 天下一二三パズル解説

8パズル、15パズルの最短経路を求める解法としては、A*アルゴリズム、タブーサーチ+最良優先探索、各ピースのマンハッタン距離を使った評価関数などを使う解法があり得ます。

しかし、8パズル、15パズルの最短経路を求めるための単純なプログラムを、そのまま123パズルに適用した場合、その盤面の大きさと空白の多さのため、探索範囲が爆発してしまうので最短経路はもちろんのこと、解答となる経路のうちの一つを見つけ出すことも出来ずに終わってしまう場合が多いはずです。

この問題を解決する方法としては、例えば、以下の二つの方針が考えられます。

1. 探索を使わない手で解くような解法をベースに短い手順を見つける。

123ピース程度のパズルであれば、十分な時間があれば手で解くことも可能です。

この解法には、まず特定の位置に対して、ダイクストラ法などを用いて、1番近い空白見つけてきて、そこまで空白を持ってくるプログラムを実装する方法があります。これを使って空白の位置を操りながら、1から順番に縦横にそろえていけば、100点を超える点数をとることができます。

さらに、以下のように、上段1段を常に空白を作っておくことで、各ピースを横方向に目的位置に近づける際の手数と実装コストを小さくすることができます。これにより、150点に近い得点をとることができます。

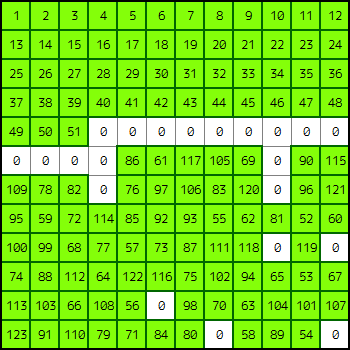
2. 各ピースのマンハッタン距離よりも良い評価関数を考えて、枝刈り探索を行う。

単純にマンハッタン距離のみを評価関数に使うとピースが上部に、空白が下部に固まってしまうような悪い盤面に対して、高い評価値が与えられてしまいます。マンハッタン距離よりも良い評価値を考えることで、この問題を解決します。

こちらの方針の方が、1.の方針よりも良い解答が得られそうに思えますが、盤面が局所解におちいらないような評価関数を作るのがかなり難しいため、実装コストが高くなると思われます。